Alertes failles
de sécurité et
de mises à jour
Contribuer - Questionner
Faire un lien
Assiste.com - Sécurité informatique - Vie privée sur le Web - Neutralité d'Internet Assiste.com - Sécurité informatique - Vie privée sur le Web - Neutralité d'Internet
 

Assiste.com

Attaque des mots de passe en force brute

Attaque en force brute : l'une des méthodes de cryptanalyse pour tenter de casser un cryptage (déchiffrer un chiffrement). Besoins matériels et temps d'attaque.

cr  10.11.2009      r+  05.11.2022      r-  27.04.2024      Pierre Pinard.         (Alertes et avis de sécurité au jour le jour)

Attaque en force brute

Attaque des mots de passe en force brute      Attaque des mots de passe en force brute      Index      Attaque des mots de passe en force brute      Attaque des mots de passe en force brute

Sécurité des mots de passe

Introduction
Liste

Malwarebytes et Kaspersky ou
Emsisoft (incluant Bitdefender)


Sommaire (montrer / masquer) 

Attaque en force brute - Attaque en force brute Attaque en force brute - 01 Attaque en force brute top top

L'attaque en force brute est l'une des méthodes utilisées en cryptanalyse pour tenter de casser un cryptage. Le principe en lui-même de l'attaque en force brute ne vise pas exclusivement les mots de passe, mais c'est dans ce domaine que ce type d'attaques est essentiellement utilisé.

Un cybercriminel s'est procuré un identifiant (login) et le hashcode du mot de passe associé à cet identifiant (ou des listes d'identifiants et les hashcodes des mots de passe associés). On ne se soucie pas du moyen mis en oeuvre pour les obtenir (piratage d'un serveur, écoute par sniffer, etc.). La question n'est pas là.

L'attaque en force brute commence lorsque l'on dispose du couple identifiant et chiffre clé dont on ne peut rien faire. Il faut remonter du chiffre clé au mot de passe d'origine. Il faut casser le chiffre clé qui normalement ne permet pas de remonter à la chaîne de caractères qui a servi à le générer puisque le cryptage du mot de passe, ou de toutes autres choses, est à sens unique (univoque). Il n'y a pas de formule pour décrypter un hashcode, il n'y a que des méthodes.

L'une des méthodes possibles est de recommencer : crypter toutes les combinaisons possibles de caractères autorisés, avec le même algorithme (MD5, SHA-1, etc.), jusqu'à obtenir un hashcode identique à celui détenu. Pour savoir quel est l'algorithme utilisé, on regarde la longueur du hashcode piraté : 16 caractères, c'est du MD5, 20 caractères c'est du SHA-1, etc.

En utilisant du matériel spécialisé (réseau botnet ou ordinateur à base de matériel spécialement développé pour les attaques en « force brute », etc.), et après un certain temps de calcul, on finit par trouver le mot de passe à l'origine du hashcode détenu. On peut alors usurper l'identité du titulaire en utilisant son couple identifiant / mot de passe.

Les attaques en force brute se heurtent au problème du temps de calcul qui :

  1. Peut prendre des années.

  2. Nécessite du matériel dont la puissance de calcul est à des prix délirants.

    Il est certain que des clusters (grappes) de machines dotées chacune de dizaines de processeurs Xéon (le même type que pour les serveurs rapides et fiables ou le minage de monnaies virtuelles) et de dizaines de processeurs graphiques monstrueusement puissants (dont certaines fonctions de calcul sont beaucoup plus rapides qu'avec les processeurs centraux), sera incommensurablement plus rapide qu'un bête PC avec un Intel CORE I7, Intel CORE I9 ou Intel CORE IX aussi rapide et overclocké qu'il soit. On peut arriver à des installations à plusieurs millions d'€ donc il faut que les comptes attaqués en vaillent le coup (mis à part les attaques en cyberguerres d'un état contre un autre état, là ou les moyens des NSA ou FAPSI sont illimités).

  3. Est totalement dépendant de la longueur des mots de passe et du jeux de caractères utilisés dans les mots de passe.

Aidez Assiste – autorisez quelques publicités et cliquez-les
Attaque en force brute - Les jeux de caractères utilisés

L'attaque en force brute est l'une des méthodes utilisées en cryptanalyse pour tenter de casser un cryptage. Le principe en lui-même de l'attaque en force brute ne vise pas exclusivement les mots de passe, mais c'est dans ce domaine que ce type d'attaques est essentiellement utilisé.

Un cybercriminel s'est procuré un identifiant (login) et le hashcode du mot de passe associé à cet identifiant (ou des listes d'identifiants et les hashcodes des mots de passe associés). On ne se soucie pas du moyen mis en oeuvre pour les obtenir (piratage d'un serveur, écoute par sniffer, etc.). La question n'est pas là.

L'attaque en force brute commence lorsque l'on dispose du couple identifiant et chiffre clé dont on ne peut rien faire. Il faut remonter du chiffre clé au mot de passe d'origine. Il faut casser le chiffre clé qui normalement ne permet pas de remonter à la chaîne de caractères qui a servi à le générer puisque le cryptage du mot de passe, ou de toutes autres choses, est à sens unique (univoque). Il n'y a pas de formule pour décrypter un hashcode, il n'y a que des méthodes.

L'une des méthodes possibles est de recommencer : crypter toutes les combinaisons possibles de caractères autorisés, avec le même algorithme (MD5, SHA-1, etc.), jusqu'à obtenir un hashcode identique à celui détenu. Pour savoir quel est l'algorithme utilisé, on regarde la longueur du hashcode piraté : 16 caractères, c'est du MD5, 20 caractères c'est du SHA-1, etc.

En utilisant du matériel spécialisé (réseau botnet ou ordinateur à base de matériel spécialement développé pour les attaques en « force brute », etc.), et après un certain temps de calcul, on finit par trouver le mot de passe à l'origine du hashcode détenu. On peut alors usurper l'identité du titulaire en utilisant son couple identifiant / mot de passe.

Les attaques en force brute se heurtent au problème du temps de calcul qui :

  1. Peut prendre des années.

  2. Nécessite du matériel dont la puissance de calcul est à des prix délirants.

    Il est certain que des clusters (grappes) de machines dotées chacune de dizaines de processeurs Xéon (le même type que pour les serveurs rapides et fiables ou le minage de monnaies virtuelles) et de dizaines de processeurs graphiques monstrueusement puissants (dont certaines fonctions de calcul sont beaucoup plus rapides qu'avec les processeurs centraux), sera incommensurablement plus rapide qu'un bête PC avec un Intel CORE I7, Intel CORE I9 ou Intel CORE IX aussi rapide et overclocké qu'il soit. On peut arriver à des installations à plusieurs millions d'€ donc il faut que les comptes attaqués en vaillent le coup (mis à part les attaques en cyberguerres d'un état contre un autre état, là ou les moyens des NSA ou FAPSI sont illimités).

  3. Est totalement dépendant de la longueur des mots de passe et du jeux de caractères utilisés dans les mots de passe.




Attaque en force brute - Les jeux de caractères utilisés Les jeux de caractères utilisés - 02 Les jeux de caractères utilisés

Pour simplifier, les jeux de caractères autorisés/utilisés par les procédures d'identification/autorisation des sites Web sont classés, arbitrairement, en 4 types (il y a bien d'autres jeux de caractères intermédiaires) :

  1. Type 1 : Les 26 lettres de l'alphabet
    Toutes les 26 lettres de l'alphabet latin, et seulement ces 26 lettres, en majuscules seulement ou en minuscules seulement. Ce jeu de caractères est très restrictif et un mot de passe court (8 à 12 caractères) est cassable en quelques secondes ou quelques minutes par attaque en force brute ou par dictionnaire ou avec des tables arc en ciel.
    ABCDEFGHIJKLMNOPQRSTUVWXYZ
    ou
    abcdefghijklmnopqrstuvwxyz

  2. Type 2 : Le type 1 augmenté des 10 chiffres
    Amplitude : 36 caractères.
    Très restrictif et cassable très rapidement.
    ABCDEFGHIJKLMNOPQRSTUVWXYZ0123456789
    ou
    abcdefghijklmnopqrstuvwxyz0123456789

  3. Type 3 : Les types 1 ou 2 ou insensibles à la case
    Amplitude : 52 ou 62 caractères.
    Peu restrictif, mais cassable assez rapidement.
    ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz
    ou
    ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789

  4. Type 4 : Le type 3 avec plus ou moins de caractères spéciaux et accentués
    Type 3 augmenté d'un nombre plus ou moins restreint de caractères spéciaux et de caractères accentués (jeu de 90 à plus de 100 caractères).
    Très restrictif et quasi pas cassable. C'est le seul type recommandé.
    Exemples de jeux de caractères :
    ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789,?;.:/!§%µ
    ou
    ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789²&é"'(-è_çà)=#{[|\^@]}^¨$£¤ù%*µ,?;.:/!§

]
Aidez Assiste – autorisez quelques publicités et cliquez-les
Attaque en force brute - Les jeux de caractères utilisés




Attaque en force brute - Calculer le nombre de combinaisons possibles Calculer le nombre de combinaisons possibles - 03 Calculer le nombre de combinaisons possibles

Le nombre de combinaisons possibles qu'il va falloir calculer est égal à :

  • Longueur maximum du mot de passe : M caractères.

  • Longueur du mot de passe : P caractères.

  • Nombre de caractères dans le jeu de caractères : N

  • Indice i qui varie de 1 à P (P devant être égal ou inférieur à M)

Le nombre de combinaisons possibles sera de : (Pi=1 x N) + (Pi=2 x N) + (Pi=3 x N) + (Pi=4 x N), etc. jusqu'à ce que i=P.

En moyenne, il faut calculer la moitié des combinaisons possibles, ce qui peut prendre plusieurs vies si le mot de passe d'origine est long.

Il faut essayer toutes les combinaisons possibles de caractères du mot de passe, selon les spécifications de l'autorité, pour finalement tomber sur un hashcode identique à celui du mot de passe.

La force brute, qui était possible avec les mots de passe courts, est devenue totalement illusoire et vouée à l'échec contre un compte sensible (banque, e-commerce, assurance, administration, etc.).

Ces autorités exigent des mots de passe longs (plus de 16 ou 18 caractères) utilisant un jeu de caractères de type 4.

Ces autorités utilisent désormais (depuis 2012) des fonctions de hashage au moins égales à SHA-256 qui produit un condensat sur 256 bits, voire des fonctions supérieures.

En sus, ces autorités utilisent (normalement) plusieurs méthodes pour empêcher les attaques en « force brute » :

  • Détection automatique de plusieurs tentatives successives de mots de passe erronés (généralement, au bout de trois échecs, le compte est bloqué pour un certain temps (15 à 30 minutes...) ou nécessite une procédure spéciale de double authentification).

  • Détection automatique de plusieurs tentatives successives de mots de passe erronés, les mots de passe tentés étant présentés de manière ordonnée. Une contre-mesure ridicule de l'attaquant le conduit à tenter les mots de passe possibles dans un ordre aléatoire, ce qui introduit quelques difficultés, aussi bien pour une attaque manuelle que pour un logiciel robot d'attaque.

  • Après un certain nombre de tentatives infructueuses (généralement 3 tentatives), le délai pour autoriser une nouvelle tentative s'allonge. En fonction de la longueur du mot de passe, les combinaisons possibles sont tellement nombreuses que le temps moyen pour tomber sur le bon mot de passe risque d'être plus long que la fin probable de l'Univers ! Seuls les mots de passe très courts ont une toute petite chance d'être cassés par cette méthode. Comme les mots de passe très courts, très simples, ne protègent que des choses sans intérêt...

  • Une méthode de défense, lorsque l'autorité d'authentification à un doute (bon mot de passe, mais précédé de nombreuses tentatives erronées) consiste à envoyer systématiquement un message du type « Erreur de mot de passe », y compris sur le bon mot de passe.

    • Si l'utilisateur est l'authentique détenteur du compte, il va insister avec son bon mot de passe que le système d'authentification laissera passer à la tentative suivante.

    • Si l'utilisateur n'est pas le détenteur du compte, il va poursuivre son attaque en « force brute », ignorant le bon mot de passe qui vient de lui glisser entre les doigts.

  • Un captcha ralentit drastiquement une attaque en « force brute » tentée manuellement et élimine définitivement une attaque robotisée.

]
Aidez Assiste – autorisez quelques publicités et cliquez-les
Attaque en force brute - Les jeux de caractères utilisés




Attaque en force brute - Matériel, cartes et processeurs pour force brute Matériel, cartes et processeurs pour force brute - 04 Matériel, cartes et processeurs pour force brute


Deep Crack - Cartes multi-processeurs spécialisées pour des attaques en Force Brute
Deep Crack - Cartes multi-processeurs spécialisées pour des attaques en « force brute »


Deep Crack - Processeurs spécialisées pour des attaques en Force Brute
Deep Crack - Processeurs spécialisées pour des attaques en « force brute »


Deep Crack - Processeurs graphiques pour des attaques en Force Brute
Deep Crack - Processeurs graphiques pour des attaques en « force brute »
Aidez Assiste – autorisez quelques publicités et cliquez-les
Attaque en force brute - Les jeux de caractères utilisés




Attaque en force brute - Attaques - Tableau d'évaluation temps/mémoire Attaques - Tableau d'évaluation temps/mémoire - 05 Attaques - Tableau d'évaluation temps/mémoire

Il y a deux méthodes initiales pour casser les mots de passe : l'attaque en force brute et l'attaque par dictionnaires exhaustifs. Chacune de ces 2 méthodes pose un problème :

  1. Les attaques en force brute nécessitent un temps de calcul en fonction du nombre de combinaisons possibles du hashcode. Ce temps, très long (plusieurs années, voire plusieurs vies) rend ce type d'attaques impossible avec les fonctions de chiffrement solides (SHA-256 et supérieures), et même avec des fonctions plus faibles.

  2. Les attaques par dictionnaires exhaustifs nécessitent un temps de constitution de ces dictionnaires, mais, une fois ces dictionnaires construits, le volume de mémoire nécessaire est monstrueux et impossible à mettre en œuvre (sauf au niveau d'un état). Il s'agirait d'avoir un véritable centre de données (data center).

On est donc confronté à un problème de temps ou un problème de volume mémoire. L'invention d'une troisième méthode, un peu plus tard, les attaques par tables arc-en-ciel, se présentera comme un compromis temps/mémoire.

Dans le tableau suivant, en rouge, les attaques « jouables – possibles » (donc signalant des mots de passe faibles en longueur et en jeu de caractères).


Type 1 : Jeu de 26 caractères (tout majuscules ou tout minuscules)

Mots de passe de :
8 caractères9 caractères10 caractères11 caractères12 caractères13 caractères14 caractères
Rang 126262626262626
Rang 2676676676676676676676
Rang 317 57617 57617 57617 57617 57617 57617 576
Rang 4456 976456 976456 976456 976456 976456 976456 976
Rang 511 881 37611 881 37611 881 37611 881 37611 881 37611 881 37611 881 376
Rang 6308 915 776308 915 776308 915 776308 915 776308 915 776308 915 776308 915 776
Rang 78 031 810 1768 031 810 1768 031 810 1768 031 810 1768 031 810 1768 031 810 1768 031 810 176
Rang 8208 827 064 576208 827 064 576208 827 064 576208 827 064 576208 827 064 576208 827 064 576208 827 064 576
Rang 95 429 503 678 9765 429 503 678 9765 429 503 678 9765 429 503 678 9765 429 503 678 9765 429 503 678 976
Rang 10141 167 095 653 376141 167 095 653 376141 167 095 653 376141 167 095 653 376141 167 095 653 376
Rang 113 670 344 486 987 7803 670 344 486 987 7803 670 344 486 987 7803 670 344 486 987 780
Rang 1295 428 956 661 682 20095 428 956 661 682 20095 428 956 661 682 200
Rang 132 481 152 873 203 740 0002 481 152 873 203 740 000
Rang 1464 509 974 703 297 200 000

Type 1 - Combinaisons possibles (mots de passe possibles)

217 180 147 1585 646 683 826 134146 813 779 479 5103 817 158 266 467 29099 246 114 928 149 5002 580 398 988 131 890 00067 090 373 691 429 000 000

Type 1 - Temps de calcul nécessaire pour construire un dictionnaire intégral (en jours) - En rouge ce qui est " jouable ".
Basé sur le matériel construit par nsa.unaligned.org en 2007.

En 2007
0
0,03
0,66
17
447
11 628
302 319
En 2009
0
0
0
1
20
517
13 463

Type 1 - Mémoire de stockage nécessaire, en teraoctets, pour un tel dictionnaire contenant "Mot de passe", Hash MD5, Hash SHA-1 (Recherches par dichotomie, Recherche par B-Tree)

9 556
254 101
6 753 434
179 406 439
4 763 813 517
126 439 550 418
3 354 518 684 571
19 112
508 202
13 506 868
358 812 877
9 527 627 033
252 879 100 837
6 709 037 369 143




Type 2 : Jeu de 36 caractères (tout majuscules ou tout minuscules + 10 chiffres)
(cas de certains algorithmes de chiffrement qui ne tiennent pas comptes des majuscules/minuscules (insensibles à la case) et mettent le mot de passe à plat - par exemple l'algorithme de chiffrement LanManager Hash sous Windows, qui commence par transformer les minuscules en majuscules)
Mots de passe de :
8 caractères9 caractères10 caractères11 caractères12 caractères13 caractères14 caractères
Rang 136363636363636
Rang 21 2961 2961 2961 2961 2961 2961 296
Rang 346 65646 65646 65646 65646 65646 65646 656
Rang 41 679 6161 679 6161 679 6161 679 6161 679 6161 679 6161 679 616
Rang 560 466 17660 466 17660 466 17660 466 17660 466 17660 466 17660 466 176
Rang 62 176 782 3362 176 782 3362 176 782 3362 176 782 3362 176 782 3362 176 782 3362 176 782 336
Rang 778 364 164 09678 364 164 09678 364 164 09678 364 164 09678 364 164 09678 364 164 09678 364 164 096
Rang 82 821 109 907 4562 821 109 907 4562 821 109 907 4562 821 109 907 4562 821 109 907 4562 821 109 907 4562 821 109 907 456
Rang 9101 559 956 668 416101 559 956 668 416101 559 956 668 416101 559 956 668 416101 559 956 668 416101 559 956 668 416
Rang 103 656 158 440 062 9803 656 158 440 062 9803 656 158 440 062 9803 656 158 440 062 9803 656 158 440 062 980
Rang 11131 621 703 842 267 000131 621 703 842 267 000131 621 703 842 267 000131 621 703 842 267 000
Rang 124 738 381 338 321 620 0004 738 381 338 321 620 0004 738 381 338 321 620 000
Rang 13170 581 728 179 578 000 000170 581 728 179 578 000 000
Rang 146 140 942 214 464 820 000 000

Type 2 - Combinaisons possibles (mots de passe possibles)

2 901 713 047 668104 461 669 716 0843 760 620 109 779 060135 382 323 952 046 0004 873 763 662 273 660 000175 455 491 841 852 000 0006 316 397 706 306 670 000 000

Type 2 - Temps de calcul nécessaire pour construire un dictionnaire intégral (en jours) - En rouge ce qui est " jouable ".
basé sur le matériel construit par nsa.unaligned.org en 2007.

En 2007
0,01
0,47
17
610
21 962
790 627
28 462 569
En 2009
0
0
1
27
976
35 139
1 265 003

Type 2 - Mémoire de stockage nécessaire, en teraoctets, pour un tel dictionnaire contenant "Mot de passe", Hash MD5, Hash SHA-1 (Recherches par dichotomie, Recherche par B-Tree)

127 675
4 700 775
172 988 525
6 362 969 226
233 940 655 789
8 597 319 100 251
315 819 885 315 333
255 351
9 401 550
345 977 050
12 725 938 451
467 881 311 578
17 194 638 200 502
631 639 770 630 667




Type 3 : Jeu de 62 caractères (majuscules + minuscules + 10 chiffres)

Mots de passe de :
8 caractères9 caractères10 caractères11 caractères12 caractères13 caractères14 caractères
Rang 162626262626262
Rang 23 8443 8443 8443 8443 8443 8443 844
Rang 3238 328238 328238 328238 328238 328238 328238 328
Rang 414 776 33614 776 33614 776 33614 776 33614 776 33614 776 33614 776 336
Rang 5916 132 832916 132 832916 132 832916 132 832916 132 832916 132 832916 132 832
Rang 656 800 235 58456 800 235 58456 800 235 58456 800 235 58456 800 235 58456 800 235 58456 800 235 584
Rang 73 521 614 606 2083 521 614 606 2083 521 614 606 2083 521 614 606 2083 521 614 606 2083 521 614 606 2083 521 614 606 208
Rang 8218 340 105 584 896218 340 105 584 896218 340 105 584 896218 340 105 584 896218 340 105 584 896218 340 105 584 896218 340 105 584 896
Rang 913 537 086 546 263 60013 537 086 546 263 60013 537 086 546 263 60013 537 086 546 263 60013 537 086 546 263 60013 537 086 546 263 600
Rang 10839 299 365 868 340 000839 299 365 868 340 000839 299 365 868 340 000839 299 365 868 340 000839 299 365 868 340 000
Rang 1152 036 560 683 837 100 00052 036 560 683 837 100 00052 036 560 683 837 100 00052 036 560 683 837 100 000
Rang 123 226 266 762 397 900 000 0003 226 266 762 397 900 000 0003 226 266 762 397 900 000 000
Rang 13200 028 539 268 670 000 000 000200 028 539 268 670 000 000 000
Rang 1412 401 769 434 657 500 000 000 000

Type 3 - Combinaisons possibles (mots de passe possibles)

221 919 451 578 09013 759 005 997 841 600853 058 371 866 182 00052 889 619 055 703 300 0003 279 156 381 453 600 000 000203 307 695 650 123 000 000 00012 605 077 130 307 700 000 000 000

Type 3 - Temps de calcul nécessaire pour construire un dictionnaire intégral (en jours) - En rouge ce qui est " jouable ".
basé sur le matériel construit par nsa.unaligned.org en 2007.

En 2007
1
62
3844
238328
14 776 336
916 132 832
56 800 235 584
En 2009
0
3
171
10 592
656 726
40 717 015
2 524 454 915

Type 3 - Mémoire de stockage nécessaire, en teraoctets, pour un tel dictionnaire contenant "Mot de passe", Hash MD5, Hash SHA-1 (Recherches par dichotomie, Recherche par B-Tree)

9 764 456
619 155 270
39 240 685 106
2 485 812 095 618
157 399 506 309 773
9 962 077 086 856 050
630 253 856 515 383 000
19 528 912
1 238 310 540
78 481 370 212
4 971 624 191 236
314 799 012 619 546
19 924 154 173 712 100
1 260 507 713 030 770 000




Type 4 : Jeu de 100 caractères (majuscules + minuscules + 10 chiffres + 38 caractères spéciaux et accentués)

Mots de passe de :
8 caractères9 caractères10 caractères11 caractères12 caractères13 caractères14 caractères
Rang 1100100100100100100100
Rang 210 00010 00010 00010 00010 00010 00010 000
Rang 31 000 0001 000 0001 000 0001 000 0001 000 0001 000 0001 000 000
Rang 4100 000 000100 000 000100 000 000100 000 000100 000 000100 000 000100 000 000
Rang 510 000 000 00010 000 000 00010 000 000 00010 000 000 00010 000 000 00010 000 000 00010 000 000 000
Rang 61 000 000 000 0001 000 000 000 0001 000 000 000 0001 000 000 000 0001 000 000 000 0001 000 000 000 0001 000 000 000 000
Rang 7100 000 000 000 000100 000 000 000 000100 000 000 000 000100 000 000 000 000100 000 000 000 000100 000 000 000 000100 000 000 000 000
Rang 810 000 000 000 000 00010 000 000 000 000 00010 000 000 000 000 00010 000 000 000 000 00010 000 000 000 000 00010 000 000 000 000 00010 000 000 000 000 000
Rang 91 000 000 000 000 000 0001 000 000 000 000 000 0001 000 000 000 000 000 0001 000 000 000 000 000 0001 000 000 000 000 000 0001 000 000 000 000 000 000
Rang 10100 000 000 000 000 000 000100 000 000 000 000 000 000100 000 000 000 000 000 000100 000 000 000 000 000 000100 000 000 000 000 000 000
Rang 1110 000 000 000 000 000 000 00010 000 000 000 000 000 000 00010 000 000 000 000 000 000 00010 000 000 000 000 000 000 000
Rang 121 000 000 000 000 000 000 000 0001 000 000 000 000 000 000 000 0001 000 000 000 000 000 000 000 000
Rang 13100 000 000 000 000 000 000 000 000100 000 000 000 000 000 000 000 000
Rang 1410 000 000 000 000 000 000 000 000 000

Type 4 - Combinaisons possibles (mots de passe possibles)

10 101 010 101 010 1001 010 101 010 101 010 000101 010 101 010 101 000 00010 101 010 101 010 100 000 0001 010 101 010 101 010 000 000 000101 010 101 010 101 000 000 000 00010 101 010 101 010 100 000 000 000 000

Type 4 - Temps de calcul nécessaire pour construire un dictionnaire intégral (en jours) - En rouge ce qui est " jouable ".
basé sur le matériel construit par nsa.unaligned.org en 2007.

En 2007464552455 166
45 516 560
4 551 656 031
455 165 603 068
45 516 560 306 818
En 2009220220 2302 022 958202 295 82420 229 582 3592 022 958 235 859

Type 4 - Mémoire de stockage nécessaire, en teraoctets, pour un tel dictionnaire contenant "Mot de passe", Hash MD5, Hash SHA-1 (Recherches par dichotomie, Recherche par B-Tree)

444 444 444
45 454 545 455
4 646 464 646 465
474 747 474 747 475
48 484 848 484 848 500
4 949 494 949 494 950 000
505 050 505 050 505 000 000
888 888 889
90 909 090 909
9 292 929 292 929
949 494 949 494 949
96 969 696 969 697 000
9 898 989 898 989 900 000
1 010 101 010 101 010 000 000
Aidez Assiste – autorisez quelques publicités et cliquez-les
Attaque en force brute - Les jeux de caractères utilisés




Attaque en force brute - Évaluation des temps d'attaques en force brute Évaluation des temps d'attaques en force brute - 06 Évaluation des temps d'attaques en force brute

Ce testeur de solidité d'un mot de passe vous invite à utiliser des majuscules, minuscules, chiffres et symboles. En fonction du jeu de caractères utilisé et de la longueur du mot de passe, le bien connu Steve Gibson (GRC - Gibson Research Corporation) vous indique combien de temps votre mot de passe va résister contre les attaques en force brute selon la puissance de l'outil d'attaque. Ces temps sont donnés pour les puissances d'attaques à l'époque de la rédaction de son outil dont la plus ancienne trace, dans la machine à remonter le temps, est au 4 juin 2011. Or les tables arc-en-ciel ont déjà été inventées depuis 1980 et considérablement améliorées en 2003. Enfin, ce type d'attaque sur un mot de passe est sans intérêt, car cela signifie que l'on n'a pas le mot de passe et que l'on tente de le deviner en testant toutes les combinaisons possibles de caractères. Or, les sites Web demandant un mot de passe ne permettent que 3 tentatives de compositions d'un mot de passe avant de rejeter le candidat temporairement (généralement 15 à 30 minutes) puis définitivement. Ce n'est pas le mot de passe qu'il faut attaquer en ligne, mais son condensat piraté et attaqué hors ligne.

Quelle est la taille de la meule de foin dans laquelle est cachée votre aiguille ?


  1. Résistance d'un mot de passe
    Combien de temps le « bon » mot de passe de 16 caractères « 4A1a&3cP7é9à§wM; » résisterait à une attaque en force brute :

    Test de solidité d'un mot de passe
    Test de solidité d'un mot de passe

    Scénario d'attaque en ligne :
    (En supposant mille suppositions (attaques) par seconde)

    14,14 millions de milliards de siècles

    Scénario d'attaque rapide hors ligne :
    (En supposant cent milliards de suppositions (attaques) par seconde)

    1,41 centaine de milliards de siècles

    Scénario de réseau de craquage massif :
    (En supposant cent mille milliards de suppositions (attaques) par seconde)

    1,41 centaine de millions de siècles


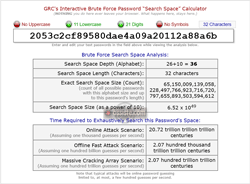
  2. Résistance d'un condensat MD5
    Combien de temps le condensat MD5 « 2053c2cf89580dae4a09a20112a88a6b » du mot de passe « 4A1a&3cP7é9à§wM; » résisterait à une attaque en force brute :

    Test de solidité d'un condensat MD5
    Test de solidité du condensat MD5 du même mot de passe « 4A1a&3cP7é9à§wM; » ci-dessus

    Scénario d'attaque en ligne :
    (En supposant mille suppositions (attaques) par seconde)

    20,72 billions de billions de billions de siècles

    Scénario d'attaque rapide hors ligne :
    (En supposant cent milliards de suppositions (attaques) par seconde)

    2,07 centaines de milliards de milliards de siècles

    Scénario de réseau de craquage massif :
    (En supposant cent mille milliards de suppositions (attaques) par seconde)

    2,07 centaines de milliards de milliards de siècles


  3. Résistance d'un condensat SHA-1
    Combien de temps le condensat SHA-1 « 35f5fdb28ab6cbe9c0b08b37e3d3bb78dfaf5066 » du mot de passe « 4A1a&3cP7é9à§wM; » résisterait à une attaque en force brute :

    Test de solidité d'un condensat SHA-1
    Test de solidité du condensat SHA-1 du même mot de passe « 4A1a&3cP7é9à§wM; » ci-dessus

    Scénario d'attaque en ligne :
    (En supposant mille suppositions (attaques) par seconde)

    58,44 billions de billions de billions de billions de siècles

    Scénario d'attaque rapide hors ligne :
    (En supposant cent milliards de suppositions (attaques) par seconde)

    5,84 centaines de milliards de milliards de milliards de siècles

    Scénario de réseau de craquage massif :
    (En supposant cent mille milliards de suppositions (attaques) par seconde)

    5,84 centaines de milliards de milliards de milliards de siècles


  4. Résistance d'un condensat SHA-256
    Combien de temps le condensat SHA-256 « 03ac2ccb14a2b14beca0048b36758dd31c5104f124f1d71c2b94056754e3d735 » du mot de passe « 4A1a&3cP7é9à§wM; » résisterait à une attaque en force brute :

    Test de solidité d'un condensat SHA-256
    Test de solidité du condensat SHA-256 du même mot de passe « 4A1a&3cP7é9à§wM; » ci-dessus

    Scénario d'attaque en ligne :
    (En supposant mille suppositions (attaques) par seconde)

    1,31 mille milliards de milliards de milliards de milliards de milliards de milliards de milliards de milliards de milliards de siècles

    Scénario d'attaque rapide hors ligne :
    (En supposant cent milliards de suppositions (attaques) par seconde)

    13,12 millions de milliards de milliards de milliards de milliards de milliards de milliards de milliards de milliards de siècles

    Scénario de réseau de craquage massif :
    (En supposant cent mille milliards de suppositions (attaques) par seconde)

    13,12 mille milliards de milliards de milliards de milliards de milliards de milliards de milliards de milliards de siècles


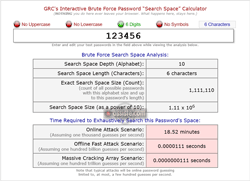
  5. Résistance d'un mot de passe imbécile
    Résistance à une attaque en force brute du mot de passe imbécile le plus utilisé au monde « 123456 ».

    Test de solidité du mot de passe imbécile le plus utilisé au monde « 123456 »
    Test de solidité du mot de passe imbécile le plus utilisé au monde « 123456 »

    Scénario d'attaque en ligne :
    (En supposant mille suppositions (attaques) par seconde)

    18.52 minutes

    Scénario d'attaque rapide hors ligne :
    (En supposant cent milliards de suppositions (attaques) par seconde)

    0.0000111 secondes

    Scénario de réseau de craquage massif :
    (En supposant cent mille milliards de suppositions (attaques) par seconde)

    0.0000000111 secondes

Aidez Assiste – autorisez quelques publicités et cliquez-les
Attaque en force brute - Les jeux de caractères utilisés




Attaque en force brute QFP (Questions fréquemment posées) - FAQ FAQ (QFP - Questions fréquemment posées)

Attaque en force brute - Autour de ce sujet dans Assiste Attaque en force brute - Autour de ce sujet dans Assiste Autour de ce sujet dans Assiste Attaque en force brute

Dossier (collection) : Mots de passe

Introduction au dossier

Concepts, attaques, défenses
16 formes d'attaques des mots de passe
Attaque en force brute
Attaque Man in the Middle
Attaque par authentification faible
Attaque par authentification frauduleuse
Attaque par caméra de surveillance
Attaque par dictionnaire exhaustif
Attaque par espionnage humain
Attaque par ingénierie sociale
Attaque par keylogger
Attaque par keylogger acoustique
Attaque par keylogger électromagnétique
Attaque par le virus PEBCAK
Attaque par phishing
Attaque par sniffing sur protocole HTTPS
Attaque par tables arc-en-ciel
Attaques célèbres et réussies de mots de passe
Décrypter un hashcode
Double authentification
Générateur de hashcode cryptographique
Générateur de mots de passe
Générateur d'identifiant (pseudo)
Heartbleed (faille dans OpenSSL) affecte les mots de passe
Identifiant
Identifier l'algorithme de hachage utilisé
Jeux de caractères utilisés dans les mots de passe
Logiciels craqueurs de mots de passe
Mot de passe
Mot de passe : test de solidité
Mots de passe imbéciles
Mots de passe par défaut (usine, constructeur, éditeur)
Risque juridique de complicité passive de l'internaute
Virer le mot de passe protégeant le BIOS

Termes (encyclopédie)
CRC
CRC-1
CRC-12
CRC-16
CRC-32
CRC-64
MD5
NTLM
SHA-1
SHA-2
SHA-224
SHA-256
SHA-384
SHA-512
BIOS
Chiffre clé
Clavier virtuel
CMOS
Condensat
Cryptographie
Exploit
Hack
Hacker
Hashcode
Heartbleed
Identifiant
Ingénierie sociale
Keylogger
Login
Mots de passe
Password Cracker
Password Revealer
Password Stealer
Phishing
Rainbow Tables (Tables Arc-en-ciel)
Spyware
UEFI

Logithèque
HashTab - Calcul de condensats (Windows)
SummerProperties - Calcul de condensats




Attaque, sécurité, informatique, force brute, mot de passe, password

Attaque en force brute - Attaque en force brute